Overwhelmed by the Covid-19 pandemic, we study the possibility of using group testing to help finding the carrier of SARS-CoV-2. (Fun fact: Covid-19 is the name of the disease; SARS-CoV-2 is the name of the virus.) The idea of group testing is simple: Suppose that there are 5 students that we want to test. We can test if each of their saliva specimens contains the virus, which will costs us 5 testing kits. We can also combine the 5 saliva specimens and test once, which will cost us 1 testing kit. If the test result is negative, then we know none of the 5 students have the virus. However, if the test result is positive, then at least one student has the virus. We then 5 more testing kits to find which of these 5 students have virus. Over all, the average cost is $1/5 + p$ testing kits per student we want to test, where $p$ is the probability that the mixture of 5 saliva specimens is positive.
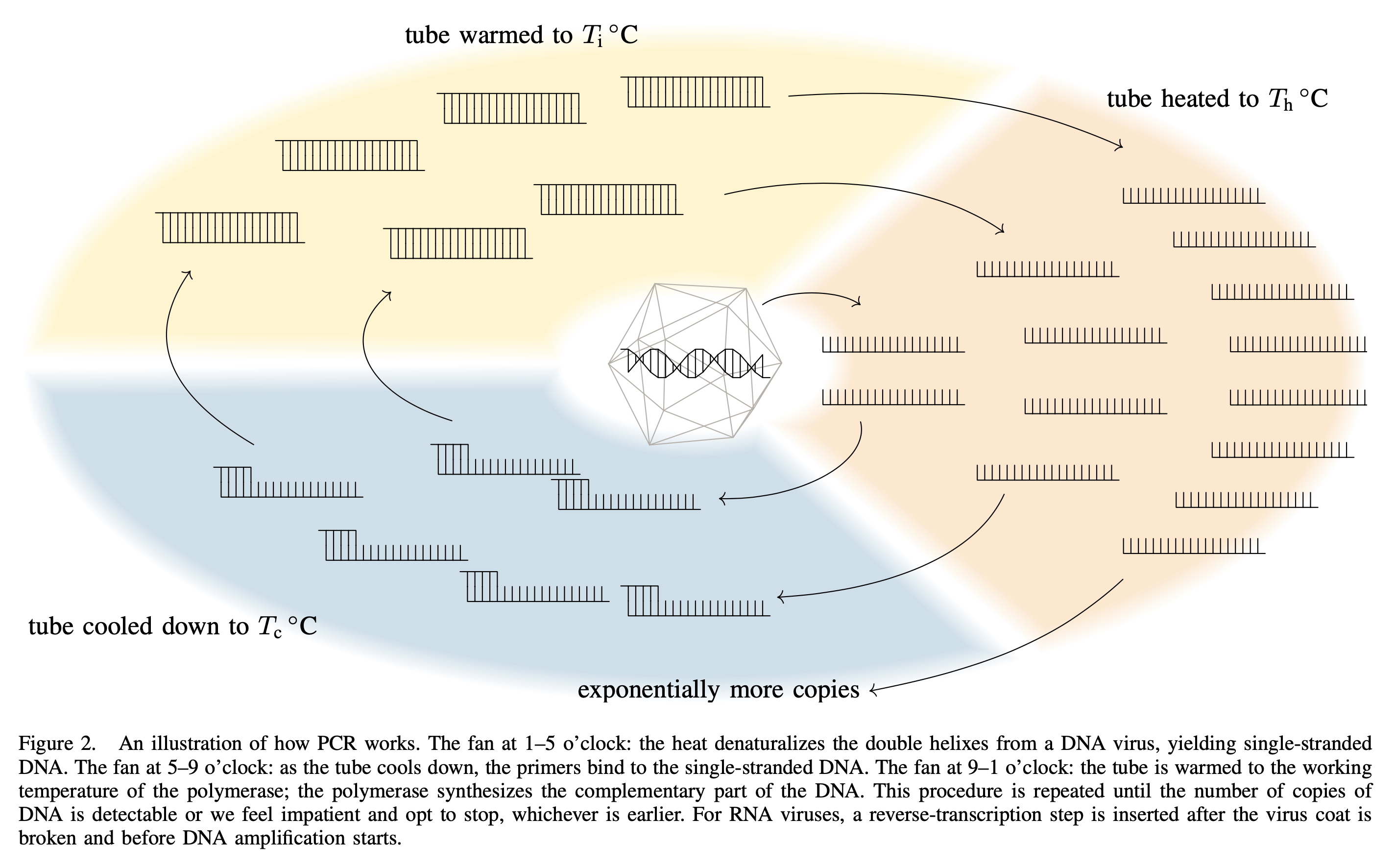
Now, one interesting aspect about testing for SARS-CoV-2 is that, in the beginning of the pandemic, this virus is so new and the whole situation is so emergency that the only reliable way is to test if a specimen contains the DNA fragments that belong to SARS-CoV-2. And the only reliable way to do so is to tell the polymerase to amplify (which is a fancy way to say duplication) the targeted fragments until the specimen contains nothing but the targeted fragments. For instance, suppose there are three types of DNA fragments, and denote the numbers of copies by $x$, $y$, and $z$, respectively. Suppose that the second type is what we are looking for; we then tell the polymerase to amplify that so the numbers of copies becomes $(x, 2y, z)$ after one cycle, $(x, 4y, z)$ after two cycles, and so on, until $2^c y$ is too large compared to $x$ and $z$ and it becomes very easy to detect. This is how PCR testing works.

A byproduct of the PCR testing is that, if a specimen contains a lot of virus particles, it would naturally contains a lot of DNA fragments and so the polymerase will need very few cycles to amplify that to a detectable degree. On the other hand, if we begin with very few DNA fragments, it would take the polymerase a lot of cycles. So by monitoring the amount of DNA fragments during amplification, we get a rough idea of the number of virus particles in a specimen. The term Ct value (which stands for cycle threshold value) is used to denote the number of cycles the polymerase needs. Let $c$ denote the Ct value and $v$ denote the number of virus particles, then $ c \approx 40 - \lfloor\log_2(v)\rfloor $ is a relation between $c$ and $v$ subject to errors.
So we want to combine group testing and Ct value. But Ct value is very nasty to work with. Naturally, if we combine a specimen with $1$ virus particle and another specimen with $1000$ virus particles, we get a mixture with $1001$ virus particles. But that’s not how Ct value works, as $1$, $1000$, and $1001$ virus particles correspond to Ct values $40$, $30$, and $30$. That is to say, a smaller Ct value tend to mask a larger Ct value to the point that it completely erases the information. Therefore, we proposed Tropical Group Testing [TropicalGT23], which is a framework to study the how group testing and Ct values should interplay.
The following is a toy example of how tropical GT works, we add specimens at different cycles to encode information.
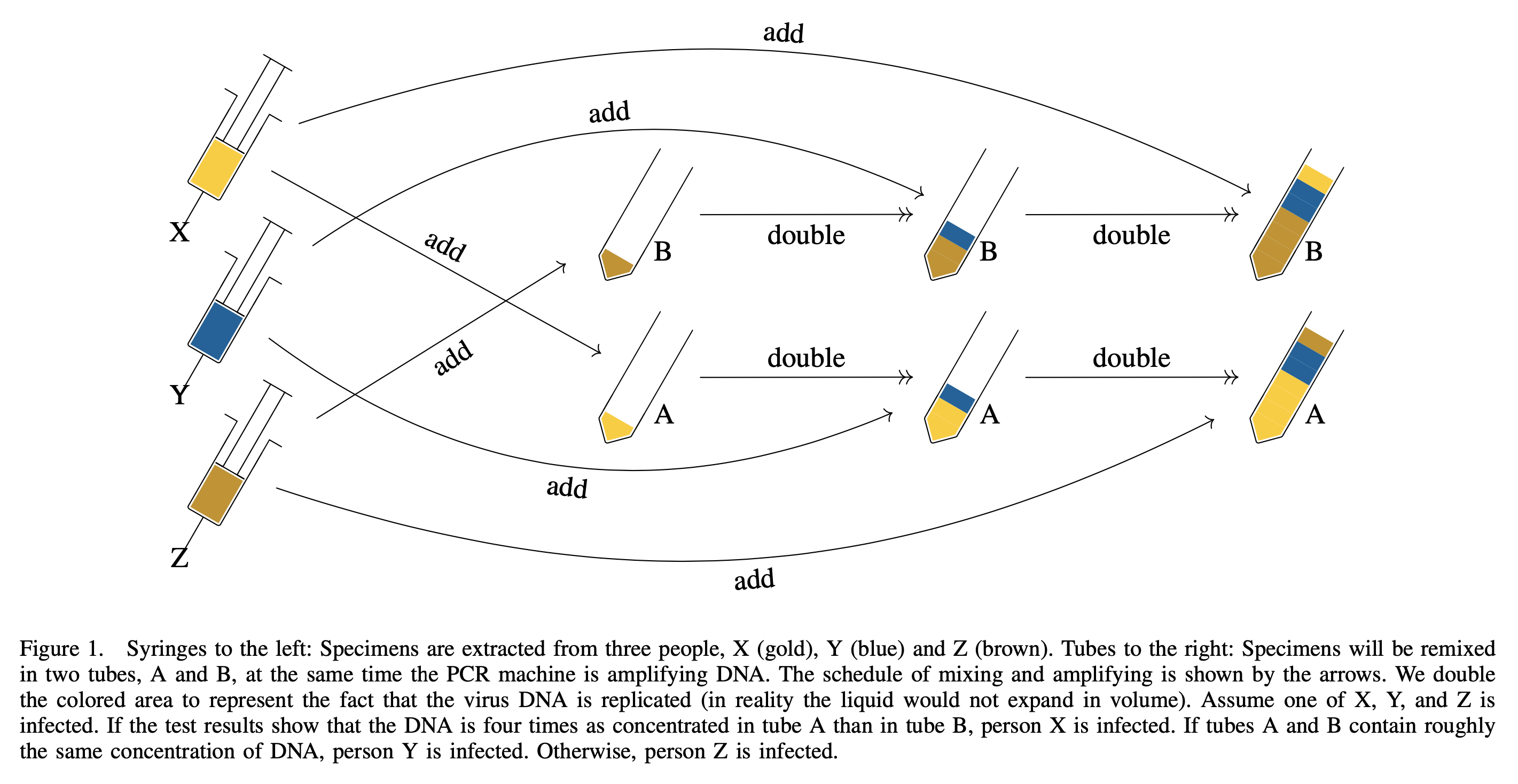
And to decode the test results, we compare those with the following figure.
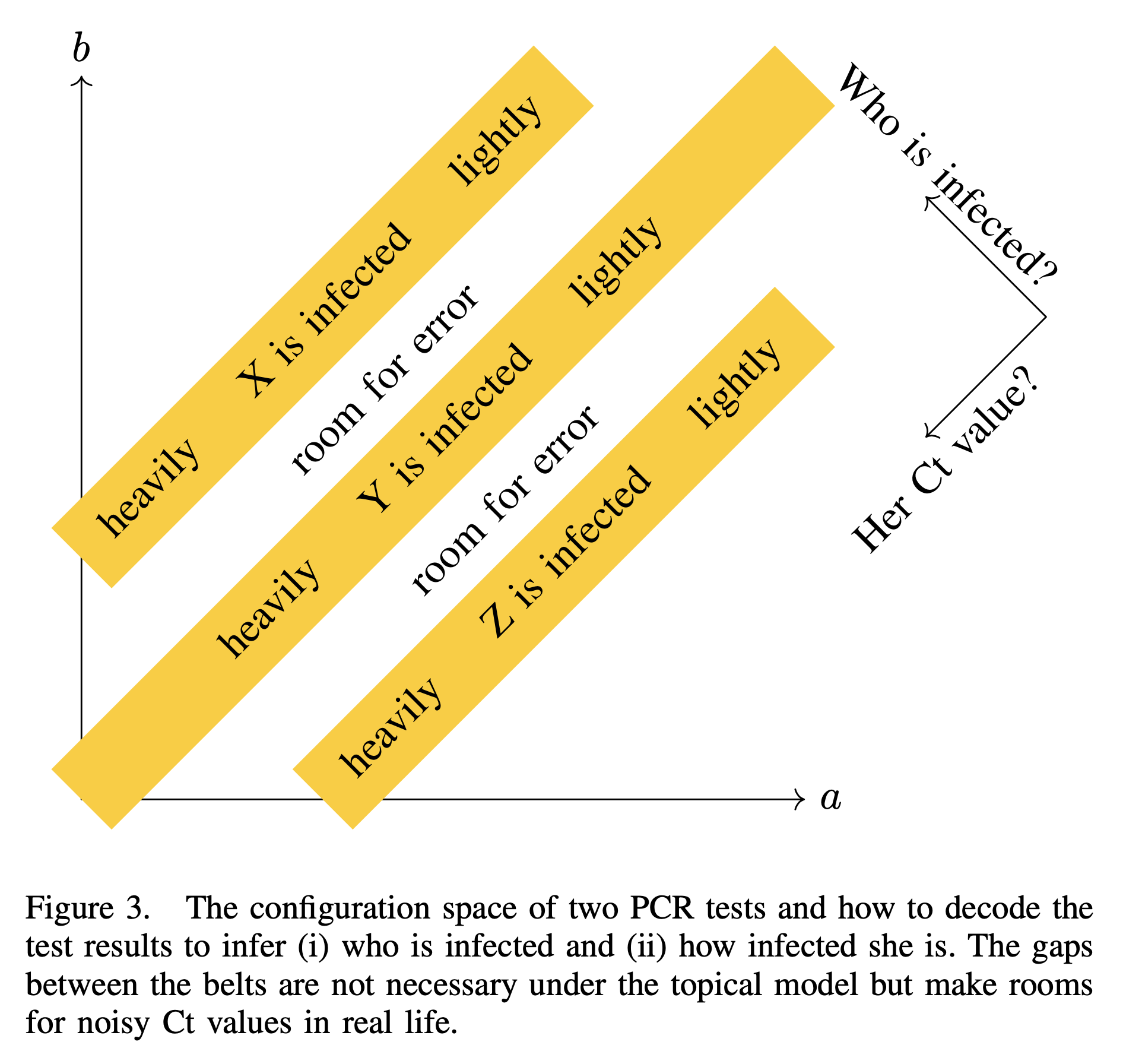
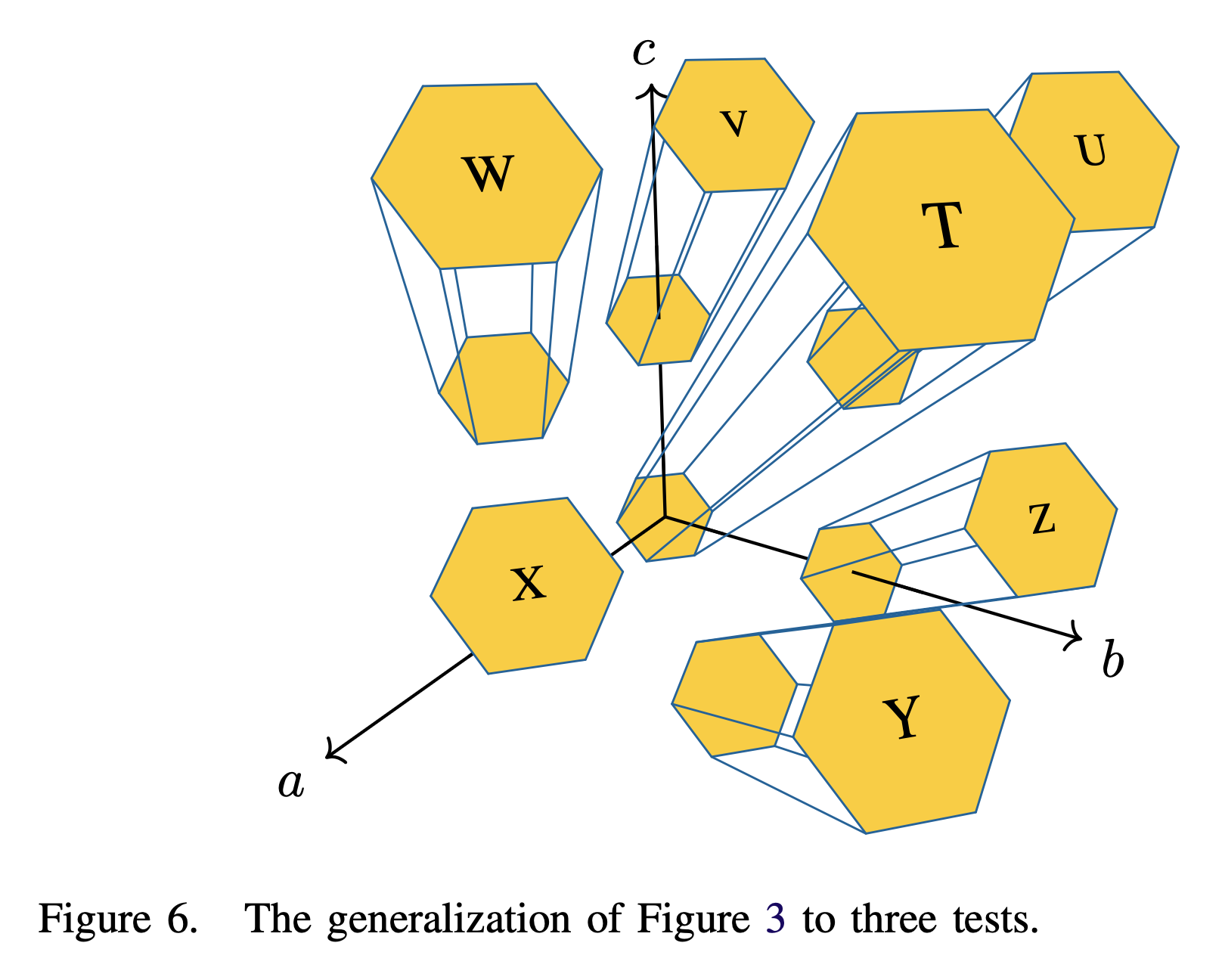
The significance of this plot is its resemblance to UCSD’s logo. I also draw a three-dimensional version for if there are three tests and seven students to be tested.
Later, when Covid-19 came to an end, we turned to more classical setting of group testing—the one with binary outputs. In [BonsaiGT23], we found that a construction of Cheraghchi–Nakos and Price–Scarlett are actually stronger than their analysis indicates. To be more precise, the question here is whether low-complexity group testing can perform as well as high-complexity group testing, and our result shows that the former is indeed almost as good as a well-studied algorithm called COMP.
The following figure summarizes how Cheraghchi–Nakos and Price–Scarlett’s decoding algorithm works.
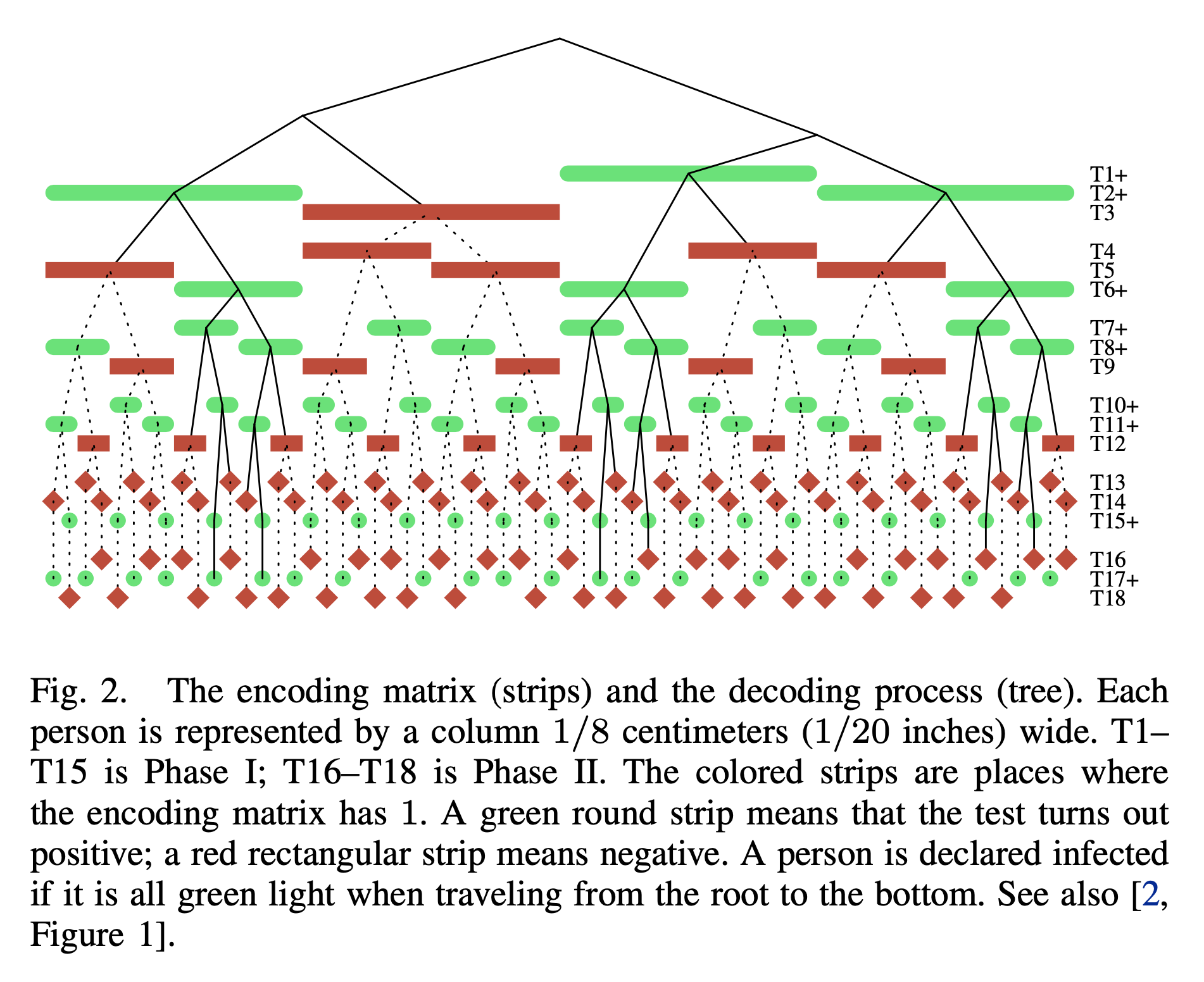
Hence the name “bonsai”.

In [Measure1Cut1-24], we study adaptive group testing. The original goal was to spend the first round of test to make some auxiliary measurements to isolate sick students; and then we spend the second round to identify the sick students. It turns out that one round for isolation is not enough unless we increase the number of tests by a huge amount. But minimizing the number of tests has a higher hierarchy than minimizing number of rounds. So we end up taking our time and cut the students in multiple rounds. That said, the identification part requires only one round and is capacity-achieving. That is, the number of tests spent here matches the predication made by measuring the entropy each test gives us.
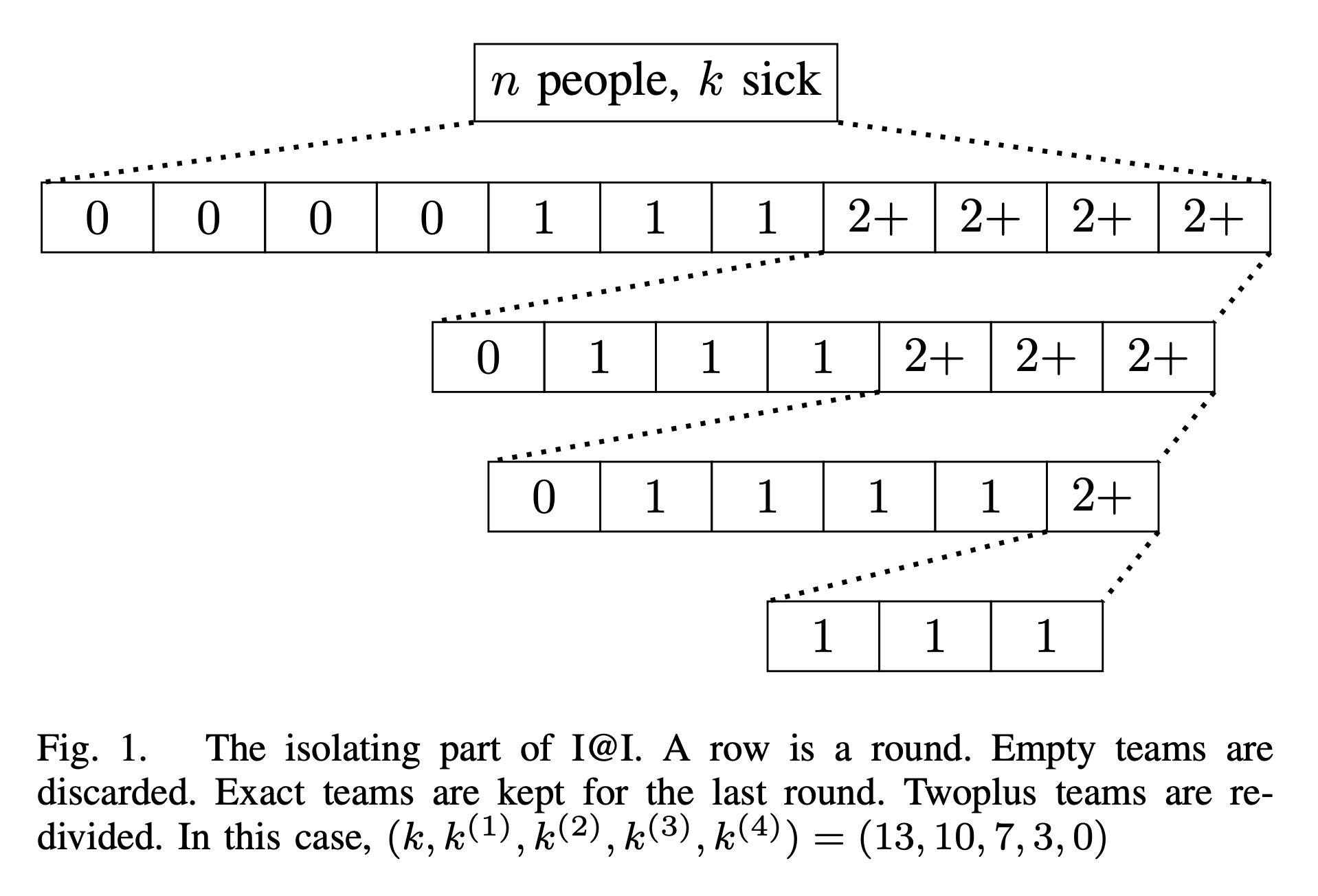
So the name “measure once, cut once” didn’t come true. That said, we are very close to the goal. The work stated that $\log k$ rounds are enough. But we conjecture that $\log(\log k)$ rounds might be enough without changing the other parameters in the existing result.