Hsin-Po's Website

Polar Code Papers

I have worked on polar coding since I was graduate student at UIUC Math.

[ModerDevia18] H.-P. Wang, I. Duursma. Polar Code Moderate Deviation: Recovering the Scaling Exponent. arXiv.
[LargeDevia18] H.-P. Wang, I. Duursma. Polar-like Codes and Asymptotic Tradeoff among Block Length, Code Rate, and Error Probability. arXiv.
[LoglogTime18] H.-P. Wang, I. Duursma. Log-logarithmic Time Pruned Polar Coding on Binary Erasure Channels. arXiv.
[LoglogTime21] H.-P. Wang, I. Duursma. Log-logarithmic Time Pruned Polar Coding. IEEE TIT.
[Hypotenuse21] H.-P. Wang, I. Duursma. Polar Codes’ Simplicity, Random Codes’ Durability. IEEE TIT.
[Dissertation21] H.-P. Wang. Complexity and Second Moment of the Mathematical Theory of Communication.
[TetraErase22] I. Duursma, R. Gabrys, V. Guruswami, T.-C. Lin, H.-P. Wang. Accelerating Polarization via Alphabet Extension. RANDOM.
[Sub-4.7-mu23] H.-P. Wang, T.-C. Lin, A. Vardy, R. Gabrys. Sub-4.7 Scaling Exponent of Polar Codes. IEEE TIT.
[DegradeWide23] H.-P. Wang, V. Guruswami. How Many Matrices Should I Prepare to Polarize Channels Optimally Fast?. ISIT.

In the early days, my research focuses on the moderate deviations principle (MDP) paradigm of noisy-channel coding. MDP addresses the asymptotic trade-offs among block length $N$ , error probability $P_{e}$ , and code rate $R$ . It is easy to show that

$P_{e} \approx \exp (- N^{π})$ ,
$Capacity - R \approx N^{- ρ}$ ,

for some positive numbers $π$ and $ρ$ . Except that the region of achievable $(π, ρ)$ -pairs as $N \to \infty$ is hard to characterize.

The MDP paradigm is a combination of the large deviations principle (LDP) paradigm and the central limit theorem (CLT) paradigm. In LDP, one cares about the asymptotic behavior of $P_{e}$ but not so much about $R$ . In the CLT paradigm, it is the opposite, that the asymptotic behavior of $R$ is studied and $P_{e}$ more or less stays constant. Both LDP and CLT are popular topics in coding community, especially for random codes. My research differs with two twists, (1) MDP studies the joint trade-offs, and (2) polar codes are low-complexity codes. The following figures from [ModerDevia18] illustrate the situation.

The gap--error plot for LDP

The gap--error plot for CLT

The gap--error plot for MDP

I got into this topic because of Mondelli, Hassani, and Urbanke’s work Unified Scaling of Polar Codes: Error Exponent, Scaling Exponent, Moderate Deviations, and Error Floors [MHU16]. This work shows that the scaling exponent of polar coding is $μ \approx 3.627$ over binary erasure channels (BECs) and $μ < 4.714$ over binary memoryless symmetric (BMS) channels. Here, the scaling exponent $μ$ is the lowest value $1 / ρ$ can take if $P_{e}$ is a constant. On top of that, this works gives a characterization of the region of $(π, ρ)$ -pairs. However, this region does not touch the point $(0, 1 / 3.627)$ for the BEC case or $(0, 1 / 4.714)$ for the BMS case, which suggests that something nontrivial happens when we make constant $P_{e}$ exponential decay.

My work [ModerDevia18] addresses the mismatch and shows that, using a complicated combinatorial counting method, the region of $(π, ρ)$ -pairs will touch $(0, 1 / 3.627)$ . Hence the slogan moderate deviations recovers the scaling exponent.

While [ModerDevia18] deals with classical polar codes as constructed in Arıkan’s original paper, [LargeDevia18] extends this theory to a wide class of polar codes. Given a kernel $K$ , its scaling exponent $μ$ , and its partial distances, we are able to predict how polar codes constructed using $K$ will behave in terms of the region of $(π, ρ)$ -pairs. Remark: This result says that it is easy to prove MDP given an estimate of $μ$ . But $μ$ is usually difficult to estimate.

Sankey's diagram

Next, I move on to encoding and decoding complexities. The following sequence of figures from [LoglogTime18] demonstrate how channel evolution works in ordinary polar codes.

Channel circuit

This is generalized to a more general tree-controlled circuit.

Pruned circuit

The idea is that, if we would like to tolerate slightly worse $P_{e}$ and $R$ , we can omit some of the green and purple boxes. This reduces the encoding and decoding complexities from $O (\log N)$ per information bit to $O (\log (\log N))$ per information bit.By worse $P_{e}$ we mean that $P_{e}$ scales as $N^{- 1 / 5}$ . By worse $R$ we that mean that $Capacity - R$ scales as $N^{- 1 / 5}$ . Note that the constructed code still achieves capacity, just not as fast as before. Here is a visualization of how many branches are left after pruning.

Pruned tree

While [LoglogTime18] deals with BECs, [LoglogTime21] handles arbitrary symmetric $p$ -ary channels, where $p$ is any prime. The main theorem in the new paper follows the recipe of the old paper—by tolerating that $P_{e}$ converges to $0$ slower and that $R$ converges to the capacity slower, we can reduce the complexity to $\log (\log N)$ per information bit.

Note that, in both [LoglogTime18] and [LoglogTime21], codes are constructed with the standard kernel $[_{1}^{1}_{1}^{0}]$ ; yet the same idea applies if a general kernel $K$ is used. What’s more, the log-log behavior generalizes to arbitrary discrete memoryless channels (DMCs). For general channels, however, the standard kernel $[_{1}^{1}_{1}^{0}]$ does not polarize anymore. So the observation that a general kernel $K$ is compatible with the log-log trick is crucial here.

Now comes my favorite work.

[Hypotenuse21] shows that it is possible to construct codes whose error probabilities and code rates scale like random codes’ and encoding and decoding complexities scale like polar codes’. On the one hand, random codes’ error and rate are considered the optimal. On the other, polar codes’ complexity ( $\log N$ ) is considered low. (Not the lowest possible complexity, as $\log (\log N)$ complexity is possible for general channels and $O (1)$ is possible for BECs.) This result holds for all DMCs, the family of channels Shannon considered in 1948.

For a figurative comparison of the region of $(π, ρ)$ , see Figure 1 on page 3 of [Hypotenuse21] (or Figure 5.4 on page 57 of [Dissertation21]).

The pi--rho plot of several milestone works

[Dissertation21] is my PhD dissertation. I summarize my earlier works and extend them a little bit.

I show that any ergodic matrix has a positive $ρ$ .
I show that you can combine [LoglogTime21] with [Hypotenuse21] to obtain a code with $ρ \approx 1 / 2$ and log-log complexity
I claim, and show with examples, that the same scaling behavior applies to distributed lossless compression and multiple access channels.

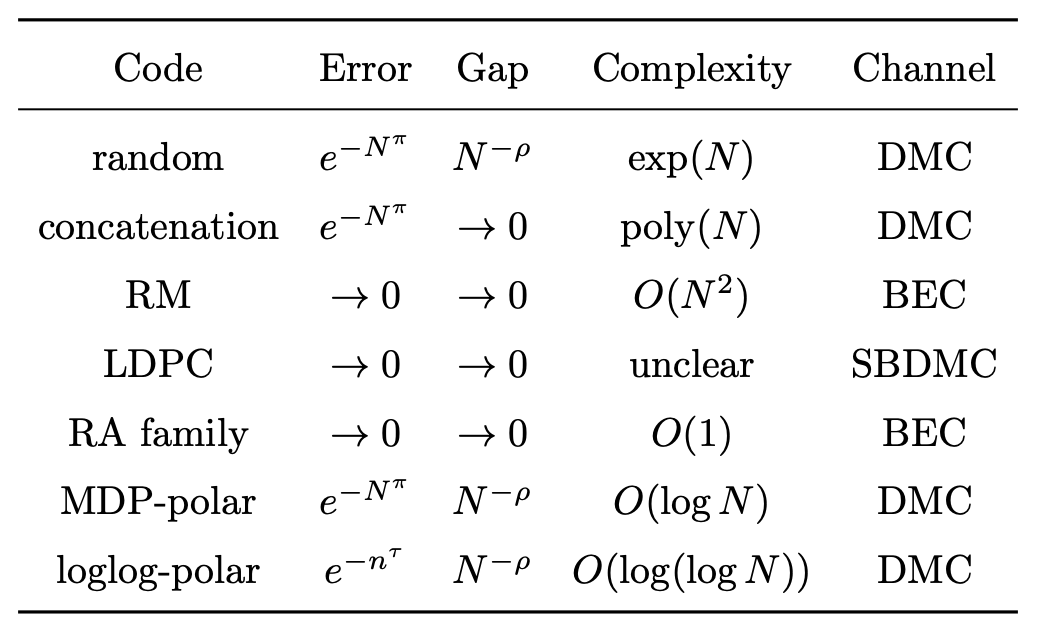
I put a lot of efforts in to my dissertation, especially to figures and tables. The following table is for channels versus goals and references. It is Table 6.1 on page 98.

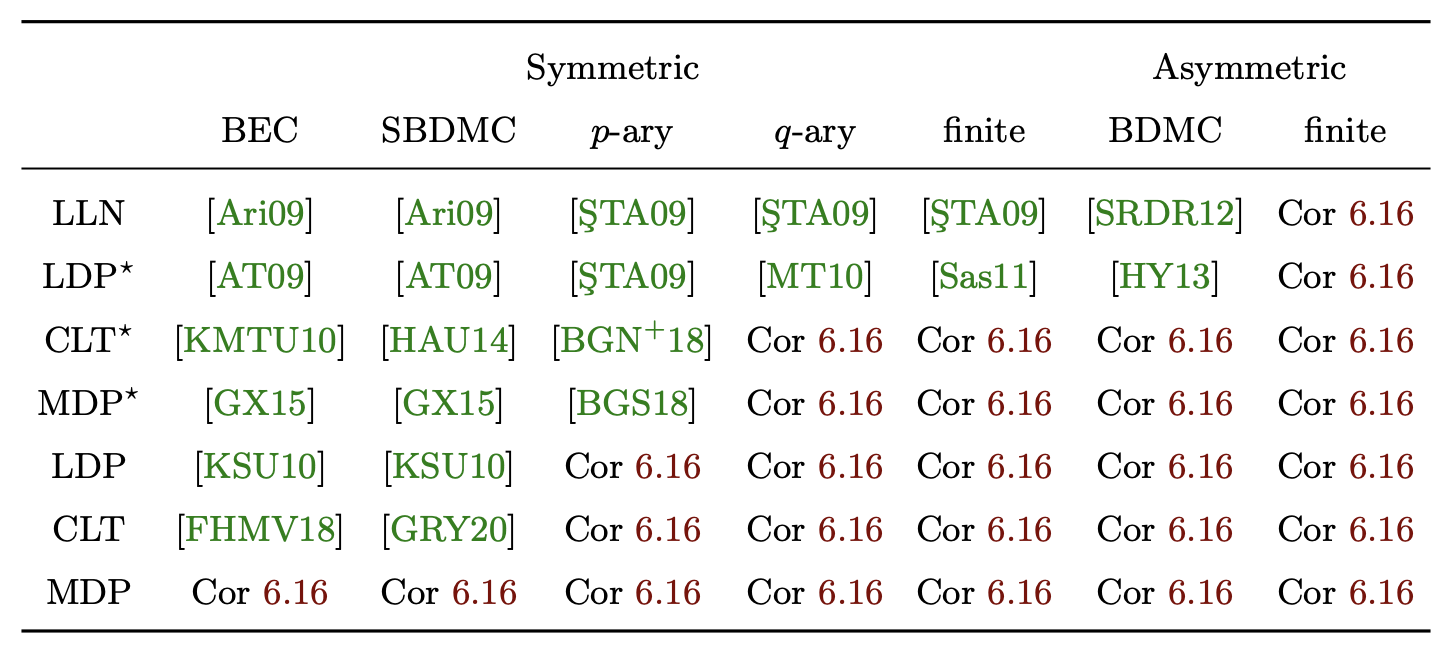
The channels, goals, and the works that achieve them

Here is a table for the error–gap–complexity trade-offs of some well-known capacity-achieving codes and the corresponding channels, obtained from Table 7.1 on page 103.

Error--gap--complexity trade-offs of some capacity-achieving codes

The following table, taken from Table 5.1 on page 55 of [Dissertation21], describes an analog among probability theory, random coding theory, and polar coding theory.

Trinitarian analogs among probability, random coding, polar coding

Binomial coefficients recover the binary entropy function; this is used in the study of minimal distances of random codes. This is Figure 6.3 on page 80.

Binomial coefficients

Binary entropy function and the KL divergences that are useful for larger alphabet has a nice upper bound $\sqrt{e q}$ . This is on page 82.

Binomial coefficients

Capacity region for distributed compression. (Page 110)

Capacity region for compression with helper

Capacity region for distributed compression. (Page 113)

Capacity region for distributed compression

Capacity region for multiple access channels. (Page 119)

Capacity region for multiple access channels

In the next two works, [Sub-4.7-mu23] and [TetraErase22], I pivot from MDP to CLT. The motivation is that, since any further improvement of MDP will come from improvement of the scaling exponent, I try to attack the latter.

[Sub-4.7-mu23] considers the standard setting of polar code: the standard kernel $[_{1}^{1}_{1}^{0}]$ over BMS channels. Before it was proved in [MHU16] that $μ < 4.71$ . We show that $μ < 4.63$ . This improvement is small, but it delivers a message that considering the iteration one at a time is not enough. In this work, we consider two iterations. We are able to show that, the first iteration will make BMS channel less BSC, and the second iteration will make use of the fact that the non-BSC channels polarize faster.

[TetraErase22] is another attempt to improve scaling exponent. But this time the target is BECs. For BECs, it is known for a long time that $μ \approx 3.627$ [MHU16]. It is also known for a long time that to improve $μ$ , one can use a larger kernel matrix $K$ [FVY19]. We go for another direction: enlarging the alphabet size. We show that, by enlarging the alphabet size from $2$ to $4$ , the scaling exponent improves from $3.627$ to $3.3$ . It would have take a $20 \times 20$ (linearly interpolated) matrix to achieve the same improvement.

Because in [TetraErase22] we need to bundle two BECs into a TEC (tetrahedron erasure channel) , I made a Euler diagram explaining various classes of channels.

Euler diagram various classes of channels